| Часть 5: вопросы 201-250 |
| 1. | Известно оптимальное решение двойственной задачи: y1=3, y2=4, y3=0. Задано приращение ресурса (II): & узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 2. | Известно оптимальное решение двойственной задачи: y1=3, y2=4, y3=0. Задано приращение ресурса (II): & узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 3. | Известно оптимальное решение двойственной задачи: y1=3, y2=4, y3=0. Задано приращение ресурса (III): & узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 4. | Известно оптимальное решение двойственной задачи: y1=3, y2=4, y3=0. Какие ресурсы исходной задачи являются дефицитными? узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 5. | Известно оптимальное решение двойственной задачи: y1=3, y2=4, y3=0. Какие ресурсы исходной задачи являются недефицитными? узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 6. | Известно оптимальное решение двойственной задачи: y1=3, y2=4, y3=0. Увеличению запаса какого ресурса соответствует максимальное возрастание оптимального значения целевой функции исходной задачи? узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 7. | Как выглядит множество точек, в которых функция F=30х1+40х2 принимает одно и то же значение h? узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 8. | Как на плоскости x1Ox2 с прямоугольной системой координат называется кривая вида a1x1+a2x2=b? узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 9. | Как найти геометрически точку, в которой целевая функция принимает оптимальное значение? узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 10. | Как формируется общая задача линейного программирования? узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 11. | Какой вектор задает направление увеличения целевой функции F=30х1+40х2? узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 12. | Какой вектор исключается из базиса и какой включается в базис при переходе к лучшему опорному плану? узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 13. | Какой величиной задается наклон прямой
 ? узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение ? узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 14. | Какой план транспортной задачи называется опорным? узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 15. | Какой план транспортной задачи называется оптимальным? узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 16. | Когда можно найти новый опорный план, лучший чем данный? узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 17. | Когда транспортная задача разрешима? узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 18. | Когда целевая функция задачи не ограничена на множестве допустимых планов? узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 19. | На рисунке приводится многоугольник решений задачи линейного программирования.

При F=30x1+40x2 оптимальной является точка В. Рассмотрим прямую F=h, где F= . Зафиксировав значение с2=40, получаем, что при с1=10 наклон прямой F=h совпадет с наклоном прямой (III). Какая точка будет оптимальной, если задать с1<10, а именно с1=10-& узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение . Зафиксировав значение с2=40, получаем, что при с1=10 наклон прямой F=h совпадет с наклоном прямой (III). Какая точка будет оптимальной, если задать с1<10, а именно с1=10-& узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 20. | На рисунке приводится многоугольник решений задачи линейного программирования. При F=30x1+40x2 оптимальной является точка В. Рассмотрим прямую F=h, где F=  . Зафиксировав значение с1=30, получаем, что при с2=30 наклон прямой F=h совпадет с наклоном прямой (II). Какая точка будет оптимальной, если задать с2<30, а именно с2=30-& узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение . Зафиксировав значение с1=30, получаем, что при с2=30 наклон прямой F=h совпадет с наклоном прямой (II). Какая точка будет оптимальной, если задать с2<30, а именно с2=30-& узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 21. | На рисунке приводится многоугольник решений задачи линейного программирования. При F=30x1+40x2 оптимальной является точка В. Рассмотрим прямую F=h, где F=  , зафиксировав значение с1=30. При с2=30 наклон прямой F=h совпадет с наклоном прямой (II). При с2=120 наклон прямой F=h совпадет с наклоном прямой (III). Каков диапазон изменения коэффициента с2, при котором точка В будет оставаться оптимальной? , зафиксировав значение с1=30. При с2=30 наклон прямой F=h совпадет с наклоном прямой (II). При с2=120 наклон прямой F=h совпадет с наклоном прямой (III). Каков диапазон изменения коэффициента с2, при котором точка В будет оставаться оптимальной?
 узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 22. | На рисунке приводится многоугольник решений задачи линейного программирования. При F=30x1+40x2 оптимальной является точка В. Рассмотрим прямую F=h, где F=  , зафиксировав значение с2=40. При с1=40 наклон прямой F=h совпадет с наклоном прямой (II). При с1=10 наклон прямой F=h совпадет с наклоном прямой (III). Каков диапазон изменения коэффициента с1, при котором точка В будет оставаться оптимальной? , зафиксировав значение с2=40. При с1=40 наклон прямой F=h совпадет с наклоном прямой (II). При с1=10 наклон прямой F=h совпадет с наклоном прямой (III). Каков диапазон изменения коэффициента с1, при котором точка В будет оставаться оптимальной?
 узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 23. | На рисунке приводится многоугольник решений задачи линейного программирования. При F=30x1+40x2 оптимальной является точка В. Рассмотрим прямую F=h, где F= . Зафиксировав значение с1=30, получаем, что при с2=120 наклон прямой F=h совпадет с наклоном прямой (III). Какая точка будет оптимальной, если задать с2>120, а именно с2=120+& узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение . Зафиксировав значение с1=30, получаем, что при с2=120 наклон прямой F=h совпадет с наклоном прямой (III). Какая точка будет оптимальной, если задать с2>120, а именно с2=120+& узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 24. | На рисунке приводится многоугольник решений задачи линейного программирования.
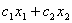
При F=30x1+40x2 оптимальной является точка В. Рассмотрим прямую F=h, где F=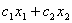 . Зафиксировав значение с2=40, получаем, что при с1=40 наклон прямой F=h совпадет с наклоном прямой(II). Какая точка будет оптимальной, если задать с1>40, а именно с1=40+& узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение . Зафиксировав значение с2=40, получаем, что при с1=40 наклон прямой F=h совпадет с наклоном прямой(II). Какая точка будет оптимальной, если задать с1>40, а именно с1=40+& узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 25. | Приведите общую математическую постановку транспортной задачи? узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 26. | Пусть значение с1 неизменно, с1=30. Каким должно быть значение с2, чтобы наклон прямой F=h, где F= 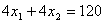 , совпал с наклоном прямой (II): , совпал с наклоном прямой (II): 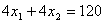 ? узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение ? узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 27. | Пусть значение с2 неизменно, с2=40. Каким должно быть значение с1, чтобы наклон прямой F=h, где F=  , совпал с наклоном прямой (II): , совпал с наклоном прямой (II):  ? узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение ? узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 28. | Пусть значение с2 неизменно, с2=40. Каким должно быть значение с1, чтобы наклон прямой F=h, где F=  , совпал с наклоном прямой (III): , совпал с наклоном прямой (III):  ? узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение ? узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 29. | Пусть значение с1 неизменно, с1=30. Каким должно быть значение с2, чтобы наклон прямой F=h, где
F= , совпал с наклоном прямой (III): , совпал с наклоном прямой (III):  ? узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение ? узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 30. | Рассматриваем задачу линейного программирования F = 30x1+40x2 & узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 31. | Рассматриваем задачу линейного программирования F = 30x1+40x2 & узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 32. | Рассматриваем задачу линейного программирования F = 30x1+40x2 & узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 33. | Рассматриваем задачу линейного программирования F = 30x1+40x2 & узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 34. | Рассматриваем задачу. Для выпуска четырех видов продукции П1, П2, П3, П4 на предприятии используют три вида сырья С1, С2, С3. В таблице приведена информация о процессе производства.
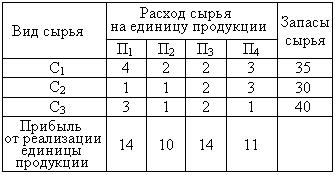
Требуется определить план выпуска продукции, обеспечивающий наибольшую прибыль. Пусть план выпуска задается величинами: x1-объем выпуска продукции вида П1; x2- объем выпуска продукции вида П2; x3- объем выпуска продукции вида П3; x4- объем выпуска продукции вида П4. Какими условиями связаны расход сырья и общее количество сырья каждого вида? узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 35. | Рассматриваем задачу. Для выпуска четырех видов продукции П1, П2, П3, П4 на предприятии используют три вида сырья С1, С2, С3. В таблице приведена информация о процессе производства.
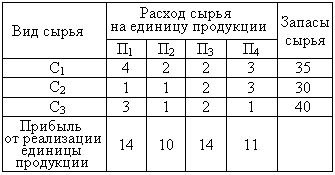
Требуется определить план выпуска продукции, обеспечивающий наибольшую прибыль. Пусть план выпуска задается величинами: x1-объем выпуска продукции вида П1; x2- объем выпуска продукции вида П2; x3- объем выпуска продукции вида П3; x4- объем выпуска продукции вида П4. Сколько будет израсходовано сырья вида C1 при таком плане выпуска? узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 36. | Рассматриваем задачу. Для выпуска четырех видов продукции П1, П2, П3, П4 на предприятии используют три вида сырья С1, С2, С3. В таблице приведена информация о процессе производства.
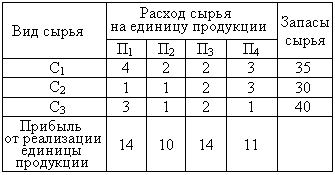
Требуется определить план выпуска продукции, обеспечивающий наибольшую прибыль. Пусть план выпуска задается величинами: x1-объем выпуска продукции вида П1; x2- объем выпуска продукции вида П2; x3- объем выпуска продукции вида П3; x4- объем выпуска продукции вида П4. Сколько будет израсходовано сырья вида C2 при таком плане выпуска? узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 37. | Рассматриваем задачу. Для выпуска четырех видов продукции П1, П2, П3, П4 на предприятии используют три вида сырья С1, С2, С3. В таблице приведена информация о процессе производства.
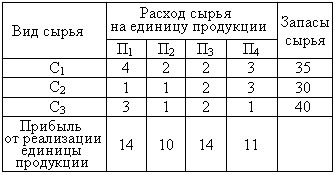
Требуется определить план выпуска продукции, обеспечивающий наибольшую прибыль. Пусть план выпуска задается величинами: x1-объем выпуска продукции вида П1; x2- объем выпуска продукции вида П2; x3- объем выпуска продукции вида П3; x4- объем выпуска продукции вида П4. Сколько будет израсходовано сырья вида C3 при таком плане выпуска? узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 38. | Рассматриваем задачу. Для выпуска четырех видов продукции П1, П2, П3, П4 на предприятии используют три вида сырья С1, С2, С3. В таблице приведена информация о процессе производства. Вид сырья Расход сырья на единицу продукции. Запасы сырья Прибыль от реализации единицы продукции
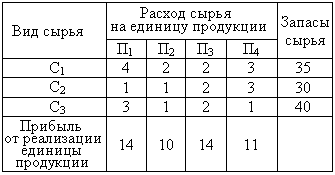
Требуется определить план выпуска продукции, обеспечивающий наибольшую прибыль. Какие неизвестные величины требуется определить в задаче? узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 39. | Рассматриваем задачу. Для выпуска четырех видов продукции П1,П2, П3, П4 на предприятии используют три вида сырья С1, С2, С3. В таблице приведена информация о процессе производства.
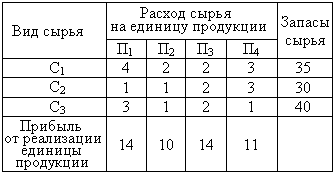
Требуется определить план выпуска продукции, обеспечивающий наибольшую прибыль. Пусть план выпуска задается величинами: x1-объем выпуска продукции вида П1; x2- объем выпуска продукции вида П2; x3- объем выпуска продукции вида П3; x4- объем выпуска продукции вида П4. Каким образом задается прибыль предприятия от реализации всех изделий? узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 40. | Рассматриваем задачу. Для производства двух видов изделий A и B предприятие использует три вида сырья. В таблице приведена информация о процессе производства.
 Учитывая,что изделия A и B могут производиться в любых соотношениях (сбыт обеспечен), требуется составить такой план их выпуска, при котором прибыль предприятия от реализации всех изделий является максимальной.Пусть план выпуска задается величинами: Учитывая,что изделия A и B могут производиться в любых соотношениях (сбыт обеспечен), требуется составить такой план их выпуска, при котором прибыль предприятия от реализации всех изделий является максимальной.Пусть план выпуска задается величинами:
x1 - количество изготовленных изделий вида A,
x2 - количество изготовленных изделий вида B.
Каким образом задается прибыль предприятия от реализации всех изделий? узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 41. | Рассматриваем задачу. Для производства двух видов изделий A и B предприятие использует три вида сырья. В таблице приведена информация о процессе производства.
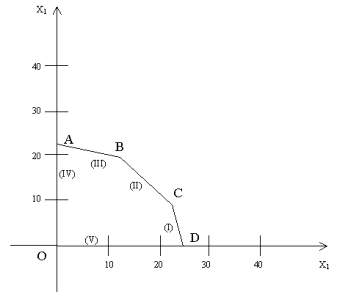
Учитывая, что изделия A и B могут производиться в любых соотношениях (сбыт обеспечен), требуется составить такой план их выпуска, при котором прибыль предприятия от реализации всех изделий является максимальной. Пусть план выпуска задается величинами: x1 - количество изготовленных изделий вида A; x2 - количество изготовленных изделий вида B.
Математической моделью данной задачи является задача линейного программирования: F = 30x1+40x2 & узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 42. | Рассматриваем задачу. Для производства двух видов изделий A и B предприятие использует три вида сырья. В таблице приведена информация о процессе производства.
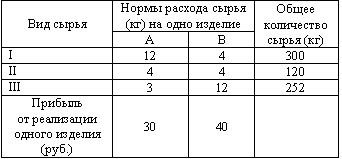
Учитывая, что изделия A и B могут производиться в любых соотношениях (сбыт обеспечен), требуется составить такой план их выпуска, при котором прибыль предприятия от реализации всех изделий является максимальной. Пусть план выпуска задается величинами:
x1 - количество изготовленных изделий вида A,
x2 - количество изготовленных изделий вида B.
Сколько будет израсходовано сырья первого вида при таком плане выпуска? узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 43. | Рассматриваем задачу. Для производства двух видов изделий A и B предприятие использует три вида сырья. В таблице приведена информация о процессе производства.
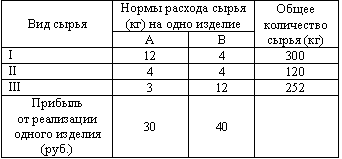
Учитывая, что изделия A и B могут производиться в любых соотношениях (сбыт обеспечен), требуется составить такой план их выпуска, при котором прибыль предприятия от реализации всех изделий является максимальной.
Пусть план выпуска задается величинами:
x1 - количество изготовленных изделий вида A,
x2 - количество изготовленных изделий вида B.
Сколько будет израсходовано сырья вида II при таком плане выпуска? узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 44. | Рассматриваем задачу. Для производства двух видов изделий A и B предприятие использует три вида сырья. В таблице приведена информация о процессе производства.
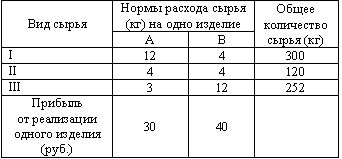
Учитывая, что изделия A и B могут производиться в любых соотношениях (сбыт обеспечен), требуется составить такой план их выпуска, при котором прибыль предприятия от реализации всех изделий является максимальной. Пусть план выпуска задается величинами:
x1 - количество изготовленных изделий вида A,
x2 - количество изготовленных изделий вида B.
Какими условиями связаны расход сырья и общее количество сырья каждого вида? узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 45. | Рассматриваем задачу. Для производства двух видов изделий A и B предприятие использует три вида сырья. В таблице приведена информация о процессе производства.
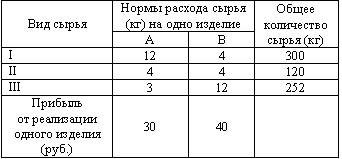
Учитывая, что изделия A и B могут производиться в любых соотношениях (сбыт обеспечен), требуется составить такой план их выпуска, при котором прибыль предприятия от реализации всех изделий является максимальной.Пусть план выпуска задается величинами:
x1 - количество изготовленных изделий вида A,
x2 - количество изготовленных изделий вида B.
Сколько будет израсходовано сырья вида III при таком плане выпуска? узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 46. | Рассматриваем задачу. Для производства двух видов изделий A и B предприятие использует три вида сырья. В таблице приведена информация о процессе производства.
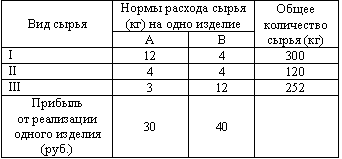
Учитывая, что изделия A и B могут производиться в любых соотношениях (сбыт обеспечен), требуется составить такой план их выпуска, при котором прибыль предприятия от реализации всех изделий является максимальной. Какие неизвестные величины требуется определить в задаче? узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 47. | Рассматривается задача линейного программирования F = 30 x1+40 x2 & узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 48. | Рассматривается задача линейного программирования F = 30x1+40x2 & узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 49. | Рассматривается задача линейного программирования F = 30x1+40x2 & узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
| 50. | Рассматривается задача линейного программирования F = 30x1+40x2& узнать ПРАВИЛЬНЫЙ ответ | добавить объяснение | |
|
![]() Здравствуйте, гость!
Здравствуйте, гость!![]() Здравствуйте, гость!
Здравствуйте, гость!